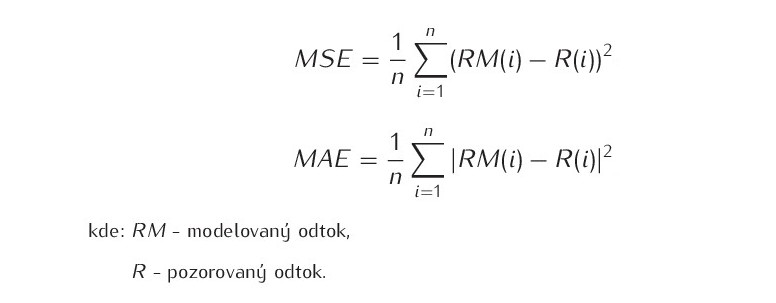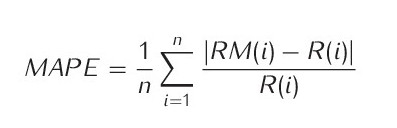Kalibrace a optimalizace parametrů
Kalibrace parametrů modelu Bilan
Parametry modelu jsou identifikovány (kalibrovány) pomocí optimalizačního algoritmu. Optimalizace je založena na hledání nejlepší shody mezi pozorovaným a modelovaným odtokem v celé časové řadě (za zvolené kalibrační období). K dispozici jsou dva optimalizační algoritmy, jeden lokální a jeden globální.
Při standardní optimalizační proceduře je odhadnutá chyba rovna standardní odchylce mezi pozorovanou a modelovanou časovou řadou, tato chyba může být použita jako optimalizační kritérium (Horáček et al., 2009). Nevýhodou volby tohoto relativně jednoduchého kritéria je fakt, že nedokáže dobře fitovat (reprodukovat) hodnoty průtoků v oblasti nízkých průtoků. Tento problém se částečně vyřeší tím, že se použijí relativní odchylky pozorované a modelované časové řady. Relativní v tomto případě znamená, že odchylky jsou rozděleny dle průměrného odtoku v jednotlivých měsících. Tento přístup vyřeší problém nízkých průtoků, avšak dochází k nezanedbatelné chybě v oblasti středních hodnot. Z těchto důvodů byla vyvinuta optimalizace, která kombinuje oba přístupy a probíhá ve dvou krocích, kdy každý krok lze nastavit individuálně (Horáček et al., 2009; Kašpárek et al., 2013).
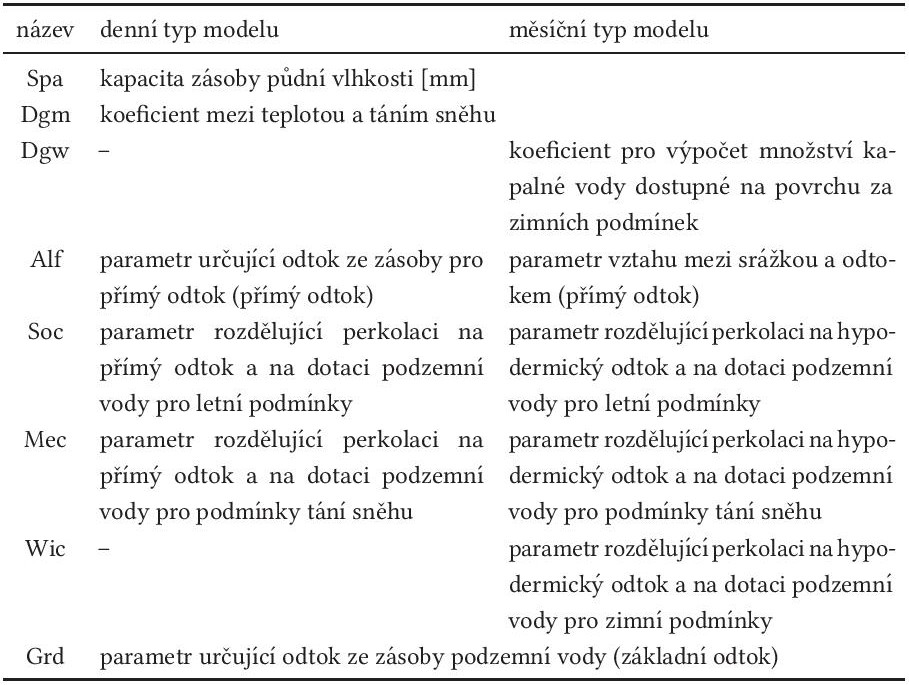
Při klasické optimalizační proceduře je v prvním kroku použita hodnota průměrné (střední) kvadratické chyby (MSE, mean square error) nebo hodnota průměrné absolutní chyby (MAE, mean absolute error). Tyto kalibrační kritéria jsou použity pro odhad parametrů Dgw, Dgm, Spa a Alf (parametry jsou popsány v tabulce 5), které reprezentují hodnoty průměrného odtoku.
Zbývající parametry modelu Wic, Mec, Soc a Grd ovlivňující distribuci odtoku do jednotlivých komponent modelu jsou kalibrovány pomocí kritéria absolutních hodnot relativních odchylek. Tento postup byl testován a přináší lepší výsledky při kalibraci modelu, jak pro nízké hodnoty průtoků, které jsou ovlivněné především hodnotou základního odtoku, tak pro střední hodnoty odtoku (Horáček et al., 2009; Kašpárek et al., 2013). Průměrná výsledná absolutní hodnota relativních odchylek je vyhodnocena pomocí optimalizačního kritéria MAPE:
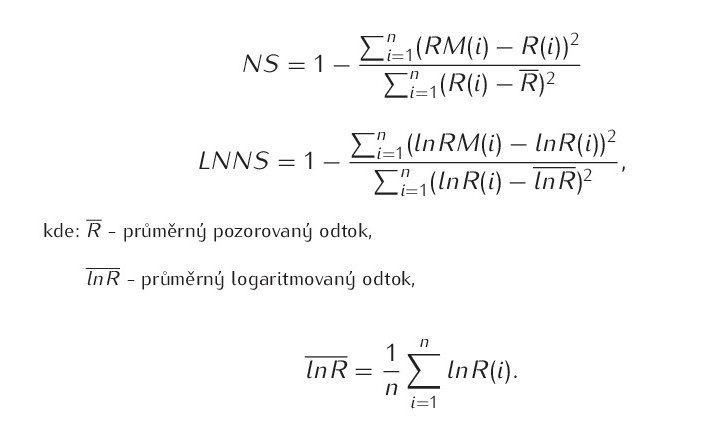
Jako optimalizační kritérium lze také použít Nash-Sutcliffe efficiency (NS) nebo logarithmic Nash-Sutcliffe (LNNS).
Model umožňuje nastavení počtu iterací, kdy je standardně přednastavená hodnota 500, Tato hodnota byla definována expertním odhadem na základě zkušeností uživatelů. Model je také možno spustit bez optimalizace, kdy se nastaví parametry napevno.
Globální optimalizační algoritmus – SCDE
Dále je možno použít pro optimalizaci parametrů modelu Bilan globální algoritmus SCDE – Shuffled Complex Differential Evolution. Metoda je odvozena z algoritmu publikovaného a testovaného v rámci studií (Vrugt et al., 2009; Mariani et al., 2011). Použitý algoritmus pracuje s populací modelů, které prostřednictvím vzájemné interakce prohledávají parametrický prostor a nacházejí v něm optimální hodnoty parametrů.
Algoritmus SCDE spojuje evoluční metodu diferenciální evoluce (Storn a Price, 1997) s algoritmem promíchávání, který tvoří podstatnou část známého široce používaného algoritmu SCE-UA (Duan et al., 1994). Populace modelů je složena z jedinců. Každý z nich je reprezentován jednou sadou parametrů a hodnotou kriteriální funkce. Pro tyto jedince je iterativně hledána optimální hodnota kriteriální funkce (Máca et al., 2013).
Váhy základního odtoku
Standardně je optimalizační kritérium počítáno z časových řad pozorovaného a modelovaného odtoku. V modelu Bilan je možno nastavit váhu základního odtoku wBF na 0-1, která nastaví optimalizaci modelu tak, aby byl v případě pozorovaného odtoku, tento odtok respektován při optimalizaci. Toto kombinované kritérium se poté vypočítá (Kašpárek et al., 2013):
Model je kalibrován na řadu neovlivněných průtoků a neřeší ovlivnění hydrologické bilance vodohospodářskými operacemi v povodí. Pro tyto potřeby je možno aplikovat simulační model vodohospodářských soustav a jako jeho vstupy využít výsledné neovlivněné řady z Bilanu nebo propojený model vodohospodářské a hydrologické bilance Bilan (Vizina a Hanel, 2011).