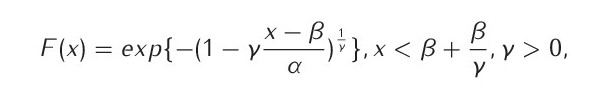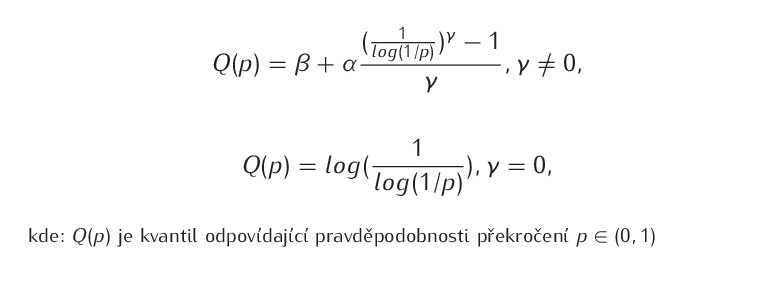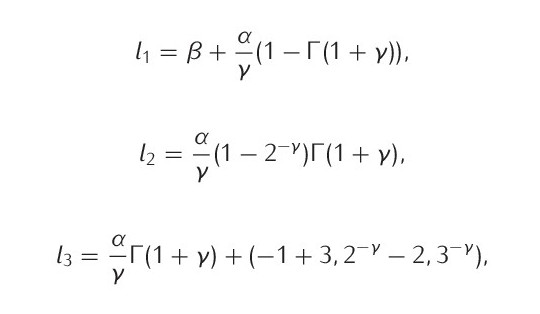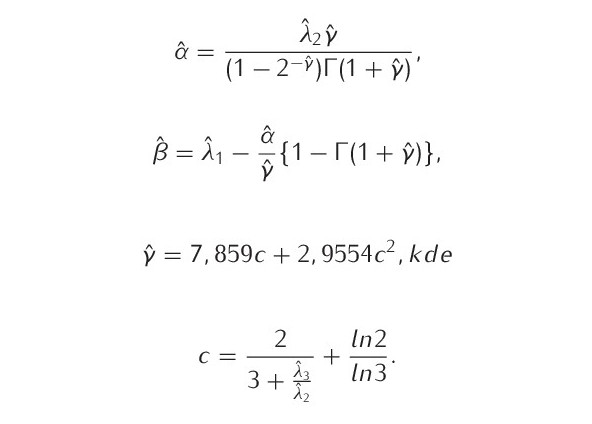Metody pro odhad parametrů
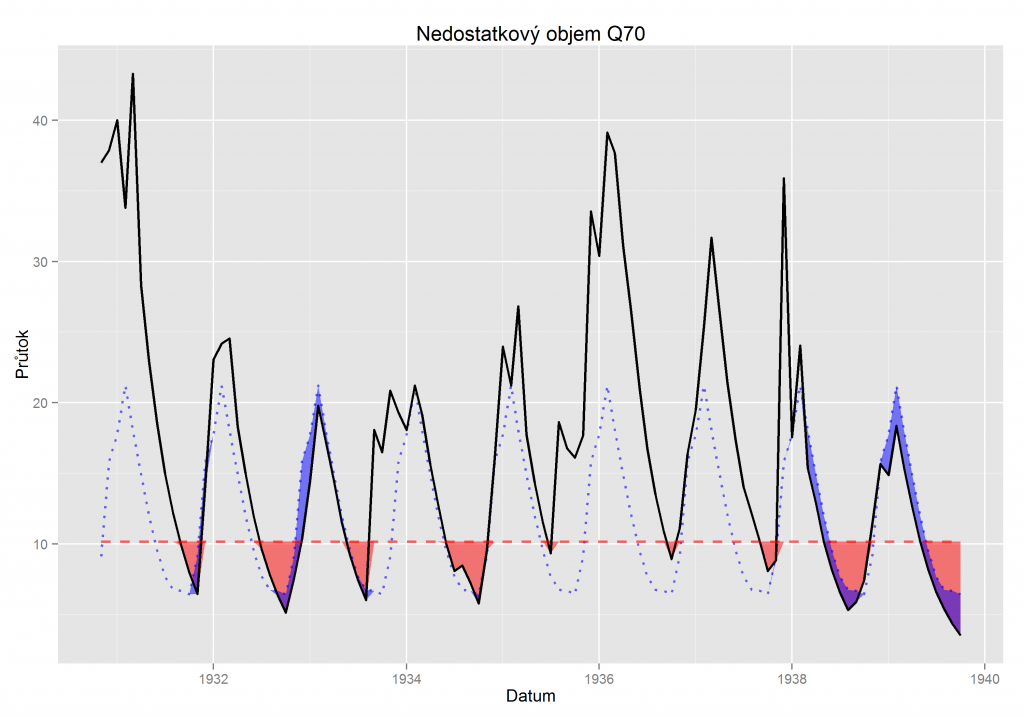
Nedostatkové objemy
Jedním z hlavních kritérií pro vyhodnocení hydrologického deficitu jsou nedostatkové objemy. Průtok je popsaný časovou funkcí Z(t). Funkce Z(t) je v čase proměnná v požadavku na vodu. Pro časový integrál <tpi, tki>, pro který je splněné podmínka Z(ti) > Q(ti) definujeme určitý integrál Wi:
Důležitým faktorem je hodnota prahu (threshold level). Bývají to kvantily průměrného ročního průtoku Q80%, Q90%, … a m-denní průtoky např. Q330, Q355 nebo Q364. V tomto případě jsou jako vstup použity denní průměrné průtoky. Avšak sucho lze posuzovat i v měsíčním časovém kroku. Měsíční průtokové řady jsou stejně přesné jako denní, pokud jsou vyhotoveny z původní denní řady.
Na obr. 2 je zobrazen příklad pro konstantní a variabilní prahové úrovně, kde se zvolilo Q70% pro konstantní úroveň a Q70% pro jednotlivé měsíce. Zavedení variabilní hodnoty je zejména důležité pro reflexi ekologických a jiných požadavků na vodní tok, avšak v současné době se v České republice většinou užívá hodnota minimálního zůstatkového průtoku, která se vypočítána z denních průtokových hodnot, a proto není použitelná pro vyhodnocení v měsíčním časovém kroku. Z tohoto důvodu byly pro vyhodnocení zvoleny průtokové kvantily Q70%, Q80%, Q90% a Q95%, a to pro konstantní i variabilní hodnotu prahu (thresholdu).
Generalized Extreme Value distribution – GEV
Pro odhad pravděpodobnosti teplotních a srážkových extrémů se běžně používá vedle dvouparametrového Gumbelova rozdělení (s parametry α, β) také tříparametrové tzv. zobecněné rozdělení extrémních hodnot (GEV–Generalized Extreme Value distribution (Jenkinson, 1969)), v němž vedle parametrů α a β vystupuje ještě třetí parametr tvaru γ. Hustota pravděpodobnosti těchto rozdělení je analyticky integrovatelná a vede k distribuční funkci (Kyselý, 2005):
Parametr γ je někdy též označovaný jako EVI index (z anglického Extreme Value Index). Hodnota parametru γ je klíčová pro analýzu extrémních hodnot, neboť určuje tvar křivky hustoty pravděpodobnosti na krajích GEV rozdělení. Gumbelovo rozdělení je tedy speciální případ GEV rozdělení s γ = 0. Zavedením třetího parametru γ u GEV rozdělení dochází ke zlepšení odhadu na pravém kraji rozdělení, pokud se extrémní hodnoty od Gumbelova rozdělení odchylují; pro γ<0( γ>0 ) se hustota pravděpodobnosti GEV rozdělení pomaleji (rychleji) přibližuje k nule ve srovnání s γ = 0 (Kyselý, 2005).
Kvantilová funkce GEV rozdělení má tvar (Polášek, 2012):
Pro přehlednost jsou zde uvedeny nejběžnější metody odhadu parametrů podle teoretického rozdělení:
- Data analytická metoda s použitím Q-Q grafu – výpočet parametrů GEV rozdělení pomocí této metody probíhá ve dvou krocích. V prvním kroku se odhaduje parametr pomocí kvantilové funkce a Q-Q grafu (Polášek, 2012).
- Metoda maximální věrohodnosti – parametry jsou hledány pomocí maximalizace věrohodnostní funkce. Věrohodnostní funkce popisuje náhodný výběr X = (x1,…, xn) a při daných hodnotách xi závisí pouze na hledaných parametrech rozdělení. Věrohodnostní funkce má tedy stejný tvar jako hustota pravděpodobnosti, ale její proměnnou není náhodná veličina X, ale parametry rozdělení. Metoda spočívá v tom, že se za odhad neznámých parametrů θ = (θ1,…,θn) považuje ten, který maximalizuje věrohodnostní funkci při daných hodnotách xi (Wilks, 2011).
- Standardní momentová metoda – je metodou pro konstrukci bodových odhadů neznámých parametrů známých rozdělení, která spočívá v tom, že porovnáváme výběrové momenty získaných dat s teoretickými momenty předpokládaného rozdělení s hustotou pravděpodobnosti f(x) (Wilks, 2011; Polášek, 2012).
- Probability weighted moment – je založena na stejném principu jako standartní momentová metoda. V tomto případě však porovnáváme „pravděpodobnostně“ vážené momenty s výběrovými momenty (Hosking et al., 1985; Diebolt et al., 2008).
- Metoda L-momentů – metoda je popsána podrobněji níže.
Metoda L-momentů
Jedná se o poměrně alternativní metodu výpočtu parametrů teoretických rozdělení, kterou navrhl Hosking (1990). Její hlavní předností je výpočetní jednoduchost a poměrně dobré výsledky pro malé a střední výběry. Metoda je vhodnější k odhadu parametrů rozdělení v praktických aplikacích (například teplotních extrémů) než metoda maximální věrohodnosti. Metodu lze doporučit pro odhad parametrů meteorologických extrémů v ČR (Kyselý 2005; Polášek, 2012).
L-momenty jsou lineární kombinace realizací vybrané proměnné, pomocí nichž lze úplně popsat jakékoli rozdělení. Výhodou této metody, oproti předchozím momentovým metodám je, že vyšší L-momenty (3 a vyšší) mohou být z výběru odhadnuty spolehlivěji a nejsou tolik citlivé na odlehlé hodnoty (Kyselý, 2005). Metoda je založena na stejném principu jako předchozí momentové metody. Porovnáváme tedy teoretické L-momenty s příslušnými odhady L-momentů. Parametry pro GEV rozdělení získáme, když první tři L-momenty l1, l2, l3, které vypadají následovně (Hosking et al., 1985; Polášek, 2012):
položíme rovny odpovídajícím odhadům ![]() Odhady parametrů
Odhady parametrů ![]() pro GEV rozdělení jsou potom dány vztahem (Hosking et al., 1985; Polášek, 2012):
pro GEV rozdělení jsou potom dány vztahem (Hosking et al., 1985; Polášek, 2012):
Využití L-momentů není omezeno pouze na odhady parametrů rozdělení. Pomocí diagramů L-momentů (například graf L-špičatosti vůči L-šikmosti) lze stanovit jakému rozdělení nejlépe vyhovují pozorovaná data. Jiné využití L-momentů je při kontrole dat nebo při testování homogenity regionů z hlediska statistických charakteristik extrémních hodnot (Kyselý, 2005; Polášek, 2012). Určení takto homogenních oblastí je nezbytné pro další moderní metodu odhadu parametrů GEV rozdělení, tzv. ROI metodu (z anglického Region Of Influence), která je vhodná pro analýzu extrémních srážkových úhrnů na stanicích (Gaál a Kyselý, 2009). ROI metoda používá k odhadu parametrů nejenom srážková data na příslušné stanici, ale také data v homogenním okolí stanice (Polášek, 2012). Pro odhad parametrů je možné použit R balík lmom (Hosking, 2014).
Kategorie dle K99
Povodí pro hodnocení vodních zdrojů jsou rozdělena dle návrhu metodiky pro výpočet minimálních zůstatkových průtoků (Mrkvičková 2013 a Balvín, 2013). Metoda vychází z rozdělení ČR podle hydrologické variability do 4 základních kategorií dle velikosti parametru K99, který je definován poměrem mezi Q99% (průtok s pravděpodobností překročení 99%) a Qa (dlouhodobý průměrný průtok). Tento poměr vyjadřuje rozkolísanost hydrologického režimu ve sledovaném profilu a byl použit jako hlavní parametr pro rozdělení ČR do jednotlivých kategorií. Pro návrh rozdělení území ČR do jednotlivých kategorií byly dále využity informace o hydrogeologických poměrech a údaje o ročním srážkovém úhrnu. Územní rozdělení bylo provedeno podle povodí, a to do úrovně čtvrtého řádu hydrologického pořadí. Základním parametrem byla hodnota K99, která byla rozdělena do 4 kategorií:
- kategorie K99, 0,18
- kategorie K99, 0,15
- kategorie K99, 0,1 – 0,15
- kategorie K99, 0,1
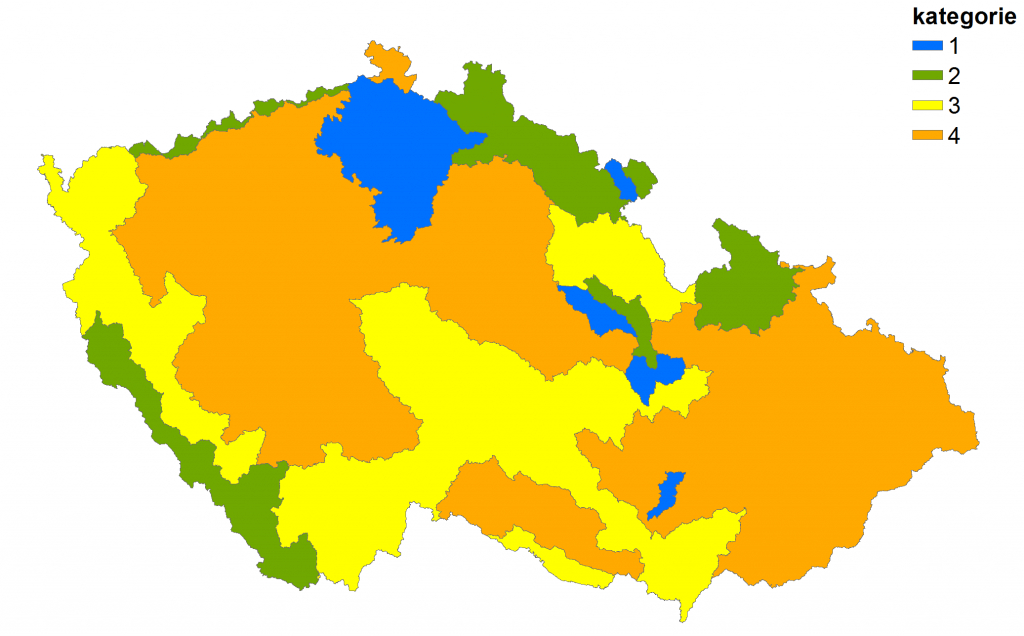
Rozdělení České republiky je uvedeno na obr. 3.
- Kategorie, reprezentuje povodí s vyrovnaným hydrologickým režimem. Do této kategorie náleží především toky nacházející se ve svrchnokřídových pánevních strukturách (pravostranné přítoky Labe, horní Metuje, Loučná, pramenné oblasti Svitavy a Třebůvky, Říčka), kde se na celkovém odtoku výrazně podílí složka základního odtoku. Roční chod průtoků v těchto oblastech se vyznačuje vyrovnaným charakterem, kdy zpravidla nedochází k výraznému poklesu průtoků na konci léta. Kategorie 1 zahrnuje povodí, pro která dosahuje parametr K99 hodnoty 0,18 a vyšší a která zároveň náleží ke křídovým hydrogeologickým strukturám.
- Kategorie, zahrnuje povodí, která leží v horských oblastech ČR. Jedná se o povodí, kde rovněž nenastávají výrazná minima v letním období. Tento fakt již není převážně způsoben hydrogeologickými podmínkami, ale souvisí s vysokým ročním srážkovým úhrnem, který zajišťuje vodnost toku během celého roku. Vzhledem k vyšší nadmořské výšce je pro oblasti v kategorii 2 dále charakteristické zpoždění v době nástupu jarního tání přibližně o měsíc oproti níže položeným oblastem. Do této kategorie byly zařazeny oblasti Krkonoš a Jizerských hor, Šumavy, Jeseníků, vrcholků Krušných hor a dále do této kategorie byla klasifikována i část povodí Tiché Orlice, která má vyrovnaný charakter pravděpodobně díky vlivu sousedních křídových povodí, kdy zde dochází k částečnému odvodňování podzemních vod z těchto struktur, i když povodí samotné již křídový charakter nemá. Hodnota K99 je pro tuto kategorii větší než 0,15. Do kategorie nebyly zařazeny oblasti na jihovýchodě Moravy (Beskydy, Javorníky), neboť i přes relativně vysokou nadmořskou výšku je roční chod průtoků ve vodních tocích rozkolísaný díky nepříznivým hydrogeologickým poměrům (převládají flyše).
- Kategorie, reprezentuje hydrologicky rozkolísanější oblasti, které je možno z hydrogeologického hlediska charakterizovat jako krystalinické struktury, které se nacházejí v podhůří pohraničních pohoří a v oblasti Českomoravské vrchoviny. Hodnota K99 pro tuto kategorii leží v intervalu 0,1-0,15.
- Kategorie, zahrnuje povodí s výrazně rozkolísaným hydrologickým režimem, která nelze jednoznačně vymezit na základě hydrogeologických podmínek. Jedná se o povodí více zranitelná vůči suchu. Hodnota K99 pro tuto kategorii je menší než 0,1.