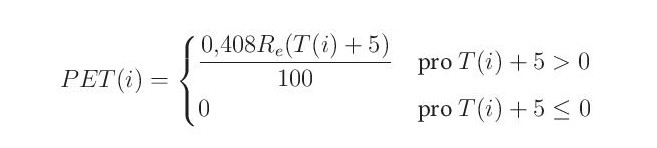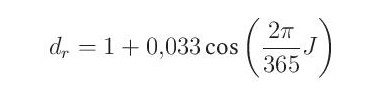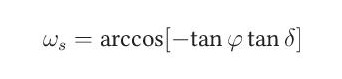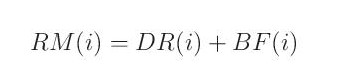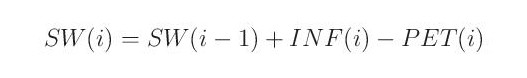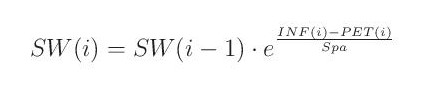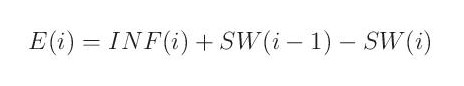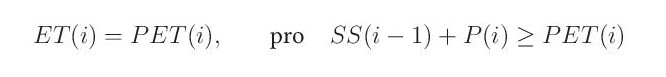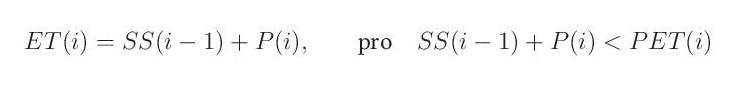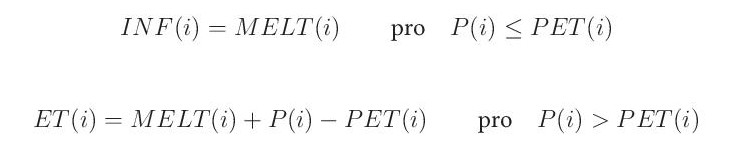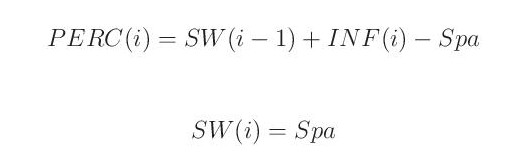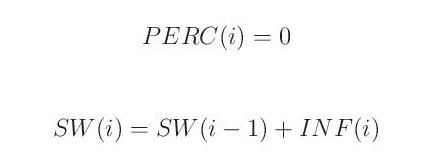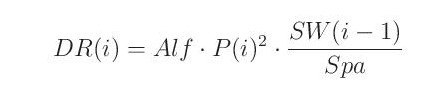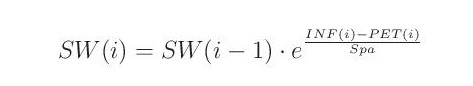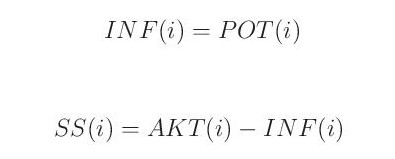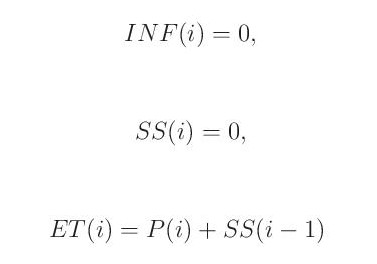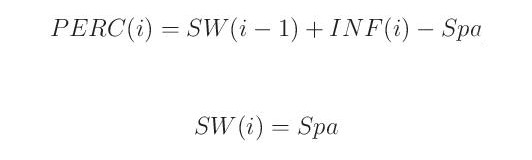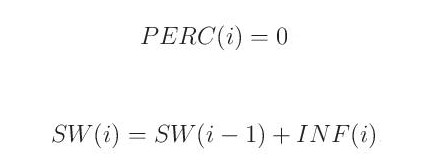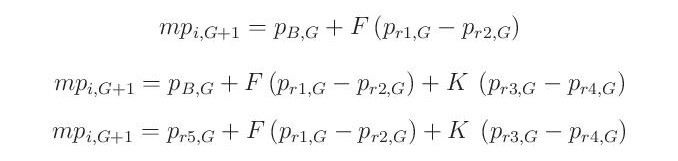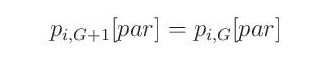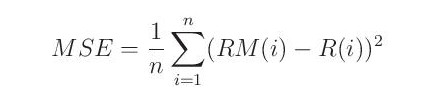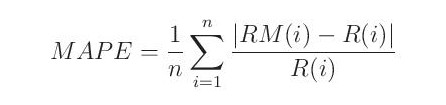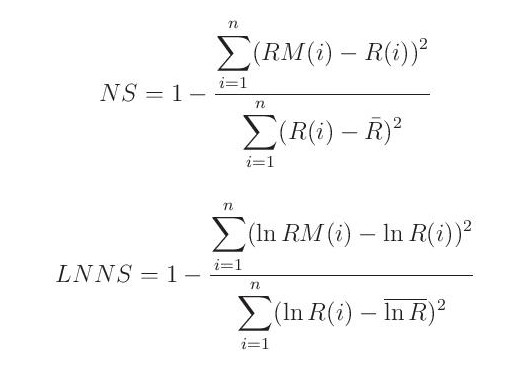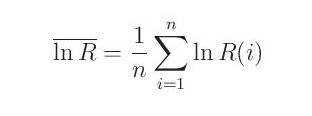Dokumentace modelu
V dokumentaci modelu je popsána jeho vnitřní struktura a jednotlivé algoritmy.
Popis Oudinovy metody pro odhad PET
Potenciální evapotranspiraci je možné odhadnout metodou odvozenou Oudinem et al. (2010). Vztah pro hodnotu PET v určitém
dni i vyžaduje jako jediný vstup teplotu vzduchu:
kde Re značí extraterestriální záření [MJ,m-2d-1], které může být zjištěno tak, jak popisují Allen et al. (1998):
kde GSC je sluneční konstanta (0,082 MJ,m-2min-1), dr inverzní relativní vzdálenost Země a Slunce
kde J je pořadové číslo dne v roce, δ značí deklinaci Slunce (úhlovou vzdálenost od rovníku) [rad]
ωs hodinový úhel západu Slunce [rad]
2 Popis denního typu modelu
2.1 Typ režimu
Použití některých algoritmů modelu závisí na podmínkách v daném dni. Model rozlišuje zimní a letní podmínky podle průměrné denní teploty vzduchu. Letní podmínky jsou uvažovány, pokud teplota
Nachází-li se na povodí sněhová pokrývka, místo algoritmu pro letní podmínky se použije algoritmus pro tání sněhu.
2.2 Složky celkového odtoku
Model simuluje celkový odtok RM(i) jako součet dvou složek:
kde DR(i) a BF(i) jsou přímý odtok a základní odtok.
Přímý odtok DR(i) představuje rychlou odezvu povodí a tvoří ho odtok ze zásoby pro přímý odtok.
Základní odtok BF(i), jehož doba zdržení na povodí je delší než u přímého odtoku, je tvořen odtokem ze zásoby podzemní vody.
Pokud jsou zahrnuty veličiny užívání vod, celkový odtok je zmenšen o odběry z povrchových vod (evidované POV(i) a neevidované PV N (i)) a zvětšen o vypouštění VY P(i). Hodnota odtoku přitom nemůže být záporná:
2.3 Územní výpar a hydrologická bilance v půdě za letních podmínek
Pokud je infiltrace, která se rovná srážkám, větší nebo rovna potenciální evapotranspiraci
územní výpar je roven potenciální evapotranspiraci
přebytek vody INF(i)-PET(i) může dotovat půdní vlhkost
a pokud je překročena kapacita zásoby půdní vlhkosti
zbývající voda perkoluje směrem dolů
a zásoba půdní vlhkosti SW (i) je rovna parametru Spa.
Převýší-li potenciální evapotranspirace srážky (infiltraci), územní výpar je dotován ze zásoby půdní vlhkosti, která se vyprazdňuje
kde e je základ přirozených logaritmů.
Územní výpar je roven součtu srážek a prázdnění zásoby půdní vlhkosti
a žádná voda neperkoluje.
2.4 Územní výpar a hydrologická bilance na povrchu za zimních podmínek
Pokud součet srážky a zásoby vody ve sněhové pokrývce převýší v daném dni potenciální evapotranspiraci, předpokládá se, že je územní výpar roven potenciální evapotranspiraci.
v opačném případě se územní výpar vypočte jako součet srážky a zásoby vody ve sněhu
Množství zbývající vody uložené ve sněhu činí
kde SS (i-1) je zásoba vody ve sněhové pokrývce ve dni i – 1.
Infiltrace je nulová
2.5 Územní výpar a hydrologická bilance na povrchu za podmínek tání sněhu
Pokud srážky převýší v daném dni potenciální evapotranspiraci, předpokládá se, že je územní výpar roven potenciální evapotranspiraci.
v opačném případě je územní výpar roven množství srážek
Množství roztálé vody v určitém dni (dostupné pro infiltraci) je dáno tepelnou kapacitou vzduchu umožňující tání sněhové pokrývky. Tato kapacita je vyjádřena jako
kde T(i) je průměrná teplota vzduchu ve dni i a Dgm je parametr vyjadřující míru tání v závislosti na teplotě vzduchu.
Zbývající zásoba vody ve sněhu je poté vypočtena jako
Voda z tání sněhu, případně ještě s přebývajícím množstvím srážek, infiltruje:
2.6 Hydrologická bilance v půdě za podmínek tání sněhu
Voda v podobě infiltrace INF(i) dotuje půdní vlhkost (nenasycenou zónu), u níž se předpokládá kapacita daná parametrem Spa. Je-li půdní kapacita překročena, přetékající voda PERC(i) perkoluje směrem dolů, tvoří přítok do zásoby pro přímý odtok a dotuje zásobu podzemní vody. Jinak řečeno, pokud je součet zásoby vody v půdě v předchozím dni SW (i-1) a infiltrace v daném dni INF(i) větší než parametr Spa, platí následující:
V opačném případě
2.7 Rozdělení perkolace na přímý odtok a dotaci podzemní vody
Perkolace PERC(i) je rozdělena na složku odtoku RDS(i), jež teče do nádrže pro přímý odtok, a na dotaci podzemní vody RC(i), jež plní zásobu podzemní vody.
ve výše uvedených rovnicích je koeficient c nahrazen pro podmínky tání sněhu parametrem Mec a pro letní podmínky parametrem Soc.
2.8 Hydrologická bilance v nádrži pro přímý odtok a přímý odtok
Zásoba pro přímý odtok DS(i) je ve dni i vypočtena jako součet zásoby v předchozím dni a přítoku RDS(i):
Přímý odtok DR(i) je představován odtokem z nádrže, který je řízen parametrem Alf
2.9 Hydrologická bilance v podzemní vodě a základní odtok
Zásoba podzemní vody GS(i) je ve dni i vypočtena jako součet zásoby v předchozím dni a dotace podzemní vody RC(i). Základní odtok je představován odtokem z podzemní vody, který je přímo úměrný zásobě na počátku daného dne a je řízen parametrem Grd
Zásoba podzemní vody na konci dne tudíž činí
Jsou-li zahrnuty veličiny užívání vod, zásoba podzemní vody je zmenšena o odběr z podzemních vod POD(i). Hodnota zásoby přitom nemůže být záporná:
3 Popis měsíčního typu modelu
3.1 Typ režimu
Použití některých algoritmů modelu závisí na podmínkách v daném měsíci. Model rozlišuje zimní a letní podmínky podle průměrné měsíční teploty vzduchu. Letní podmínky jsou uvažovány, pokud teplota
Nachází-li se na povodí sněhová pokrývka, místo algoritmu pro letní podmínky se použije algoritmus pro tání sněhu.
3.2 Složky celkového odtoku
Model simuluje celkový odtok RM(i) jako součet tří složek:
kde DR(i), I(i) a BF(i) jsou přímý odtok, hypodermický odtok a základní odtok.
Složka DR(i) celkového odtoku zahrnuje letní povrchový odtok a tu část hypodermického odtoku, která spolu s povrchových odtokem odtéká tak rychle, že neovlivňuje hydrologickou bilanci ani není ve významnější míře dostupná pro výpar. Letní přímý odtok je způsoben dešti s velkou intenzitou.
Ve všech ročních obdobích se z přebývající vody v nenasycené zóně tvoří hypodermický odtok I(i). Předpokládá se, že tato složka odtoku zahrnuje také povrchový odtok, pokud nastává v zimě nebo během období tání sněhu.
Základní odtok BF(i), jehož doba zdržení na povodí je delší než ostatních složek odtoku, je tvořen odtokem ze zásoby podzemní vody.
Pokud jsou zahrnuty veličiny užívání vod, celkový odtok je zmenšen o odběry z povrchových vod (evidované POV(i) a neevidované PVN (i)) a zvětšen o vypouštění VYP(i). Hodnota odtoku přitom nemůže být záporná:
3.3 Tvorba přímého odtoku za letních podmínek
Přímý odtok nastává v letním období jako důsledek dešťů s velkou intenzitou a je vypočten jako
kde Alf je parametr kvadratického srážkoodtokového vztahu mezi přímým odtokem a srážkami, P(i) jsou srážky v měsíci i, SW(i-1) je půdní vlhkost v měsíci i-1 a Spa parametr vyjadřující kapacitu půdní vlhkosti.
Srážky zmenšené o přímý odtok
se stávají složkou hydrologické bilance v nenasycené zóně.
3.4 Územní výpar a hydrologická bilance v půdě za letních podmínek
Pokud jsou srážky bez přímého odtoku INF(i), vypočtené rovnicí, větší nebo rovny potenciální evapotranspiraci
územní výpar je roven potenciální evapotranspiraci
přebytek vody INF(i)-PET(i) může dotovat půdní vlhkost
a pokud je překročena kapacita zásoby půdní vlhkosti
zbývající voda perkoluje směrem dolů
a zásoba půdní vlhkosti SW(i) je rovna parametru Spa.
Převýší-li potenciální evapotranspirace srážky zmenšené o přímý odtok, územní výpar je dotován ze zásoby půdní vlhkosti, která se vyprazdňuje:
kde e je základ přirozených logaritmů.
Územní výpar je roven součtu zmenšených srážek a prázdnění zásoby půdní vlhkosti
a žádná voda neperkoluje.
3.5 Územní výpar a hydrologická bilance na povrchu za zimních podmínek a za podmínek tání sněhu
Pokud součet srážky a zásoby vody ve sněhové pokrývce převýší v daném měsíci potenciální evapotranspiraci, předpokládá se, že je územní výpar roven potenciální evapotranspiraci.
Množství zbývající vody, která je potenciálně dostupná pro infiltraci (disponibilní voda ve formě sněhu), je
kde SS(i-1) je zásoba vody ve sněhové pokrývce v měsíci i-1.
Skutečné množství vody dostupné pro infiltraci je však omezeno tepelnou kapacitou vzduchu umožňující tání sněhové pokrývky v daném měsíci. Tato kapacita je za podmínek tání sněhu vyjádřena jako
kde T(i) je průměrná teplota vzduchu v měsíci i a Dgm je parametr vyjadřující míru tání v závislosti na teplotě vzduchu.
Pokud za zimních podmínek přesáhne měsíční teplota vzduchu určitou hodnotu nastavenou implicitně na Tepk = -8°C, předpokládá se, že je část srážek tvořena deštěm nebo že stávající sněhová pokrývka částečně roztaje.
Množství vody dostupné v kapalné formě je pak znovu určeno pomocí teploty vzduchu
a řízeno parametrem Dgw.
Pokud je průměrná měsíční teplota vzduchu nižší než hodnota Tepk, hydrologickou bilanci na povrchu popisuje následující rovnice:
a INF(i) = 0, tedy žádná voda neinfiltruje do půdy a rozdíl mezi srážkami a potenciální evapotranspirací doplňuje zásobu vody ve sněhu.
Pokud za zimních podmínek i podmínek tání sněhu převýší disponibilní voda AKT(i) mezní hodnotu POT(i), množství AKT(i) se rozdělí na část, která infiltruje INF(i), a na vodu, která zůstane na povrchu jako sněhová pokrývka. Platí tedy následující:
Pokud mezní hodnota POT(i) převýší množství disponibilní vody, infiltruje veškerá tato voda
a zásoba vody ve sněhové pokrývce je nulová.
Výjimečně může být hodnota AKT(i) záporná, a to tehdy, jestliže je součet srážek a zásoby vody ve sněhu v daném měsíci menší než potenciální evapotranspirace. Poté platí:
3.6 Hydrologická bilance v půdě za zimních podmínek a podmínek tání sněhu
Voda v podobě infiltrace INF(i) dotuje půdní vlhkost (nenasycenou zónu), u níž se předpokládá kapacita daná parametrem Spa. Je-li půdní kapacita překročena, přetékající voda PERC(i) perkoluje směrem dolů a dotuje zásobu podzemní vody a hypodermický odtok. Jinak řečeno, pokud je součet zásoby vody v půdě v předchozím měsíci SW(i-1) a infiltrace v daném měsíci INF(i) větší než parametr Spa, platí následující:
V opačném případě
3.7 Rozdělení perkolace na hypodermický odtok a dotaci podzemní vody
Perkolace PERC(i) je rozdělena na složku odtoku I(i), jež v daném měsíci doteče do koryta vodního toku, a na dotaci podzemní vody RC(i), jež plní zásobu podzemní vody.
ve výše uvedených rovnicích je koeficient c nahrazen pro zimní podmínky parametrem Wic, pro podmínky tání sněhu parametrem Mec a pro letní podmínky parametrem Soc.
3.8 Hydrologická bilance v podzemní vodě a základní odtok
Zásoba podzemní vody GS(i) je v měsíci i vypočtena jako součet zásoby v předchozím měsíci a dotace podzemní vody RC(i). Základní odtok je představován odtokem z podzemní vody, který je přímo úměrný zásobě na počátku daného měsíce a je řízen parametrem Grd:
Zásoba podzemní vody na konci měsíce tudíž činí
Jsou-li zahrnuty veličiny užívání vod, zásoba podzemní vody je zmenšena o odběr z podzemních vod POD(i). Hodnota zásoby přitom nemůže být záporná:
4 Popis optimalizačního algoritmu SCE-UA
Použitý globální algoritmus kombinuje metodu SCE-UA (shuffled complex evolution — The University of Arizona) popsanou Duanem et al. (1994), pro evoluci komplexu se využívá metoda diferenciální evoluce (DE), kterou popsali Storn a Price (1997).
Algoritmus obsahuje následující kroky:
- Je vygenerována populace sad parametrů (bodů) o dané velikosti NP, a to pomocí vzorkování Latin Hypercube se zadanými dolními a horními mezemi parametrů.
- Sady parametrů se seřadí podle hodnoty kritéria.
- Sady parametrů se rozdělí na NC komplexů, každý komplex obsahuje M sad. Nejlepší hodnota kritéria sady p1 je přiřazena prvnímu komplexu C1, druhá hodnota kritéria p2 komplexu C2 atd., komplex C1 tedy obsahuje sady p1, pNC+1 až p(M-1) . NC+1.
- Komplexy se vyvíjejí metodou diferenciální evoluce.
- Z vyvinutých komplexů je vytvořena nová populace.
- Algoritmus skončí po dosažení maximálního počtu iterací. V opačném případě pokračuje krokem 2.
Algoritmus diferenciální evoluce pro evoluci komplexu (krok 4) lze popsat následovně:
- Nejlepší sada parametrů z celé populace pB nebo náhodně zvolená sada parametrů pr5 je zmutována s využitím rozdílu mezi sadami parametrů náhodně zvolenými z komplexu. K dispozici jsou tři typy mutace:
kde G a G+1 značí rodičovskou generaci a generaci potomků, F a K jsou parametry mutace a r1, r2……r5 jsou indexy náhodných sad parametrů z komplexu.
- Pokud u určitého parametru par překročí pravděpodobnost křížení parametr křížení CR, potomku se přiřadí hodnota parametru zmutované sady:
Kromě pravděpodobnostního křížení závislého na CR se potomku vždy přiřadí zmutovaná hodnota jednoho parametru o náhodném indexu i.
V dalších případech, případně nachází-li se zmutovaný parametr mimo své meze a je nastaveno zamítání takových hodnot, se potomku přiřadí hodnota rodičovského parametru:
- Výběr: jestliže hodnota kritéria je lepší pro sadu parametrů potomka než pro rodiče, potomkovi se přiřadí tato nová sada, jinak jsou potomkovi přiřazeny původní parametry rodiče.
Algoritmus lze označovat názvy složenými z typu sady parametrů, která má být zmutována (best/rand), počtu rozdílů mezi parametry využitého k mutaci (1/2) a typu křížení (binomial). Rovnice 72 tak představuje typ best/1/bin, rovnice 73 typ best/2/bin a rovnice 74 typ rand/2/bin.
5 Popis kriteriálních funkcí
Střední kvadratická chyba (MSE) je průměr čtverců odchylek mezi pozorovanou a simulovanou řadou odtoku:
Střední absolutní chyba (MAE) je vypočtena jako průměr absolutních odchylek mezi pozorovanou a simulovanou řadou odtoku. „Absolutní“znamená, že záporné hodnoty jsou převedeny na kladné:
Střední absolutní procentuální chyba (MAPE) představuje průměr relativních odchylek. „Relativní“znamená, že každá odchylka je vydělena pozorovanou hodnotou:
Z této definice vyplývá, že MAPE nelze použít, pokud se vyskytují nulové hodnoty odtoku.
Použít lze také Nashův-Sutcliffův koeficient (NS) nebo logaritmický Nashův-Sutcliffův koeficient (LNNS):
kde R je průměrný pozorovaný odtok a ln R je průměr logaritmované řady odtoku: